Игра "Жизнь" и преобразование Фурье

Многие слышали о великом и ужасном быстром преобразовании Фурье (БПФ / FFT - fast fourier transform) - но как его можно применять для решения практических задач за исключением JPEG/MPEG сжатия и разложения звука по частотам (эквалайзеры и проч.) - зачастую остается неясным вопросом.

Недавно я наткнулся на интересную реализацию игры "Жизнь" Конвея, использующую быстрое преобразование Фурье - и надеюсь, оно поможет вам понять применимость этого алгоритма в весьма неожиданных местах.

Правила

Вспомним правила классической "Жизни" - на поле с квадратными клетками, живая клетка погибает если у неё больше 3 или меньше 2 соседей, и если у пустой клетки ровно 3 соседей - она рождается. Соответственно, для эффективной реализации алгоритма нужно быстро считать количество соседей вокруг клетки.

Алгоритмов для этого существует целая куча (в том числе и моя JS реализация). Но есть у задачи и математическое решение, которое может давать хорошую скорость для плотно заполненных полей, и быстро уходит в отрыв с ростом сложности правил и площади/объема суммирования - например в Smoothlife-подобных (1,2), и 3D вариантах.

Реализация на БПФ

Идея алгоритма следующая:

Формируем матрицу суммирования (filter), где 1 стоят в ячейках, сумму которых нам нужно получить (8 единиц, остальные нули) . Выполняем над матрицей прямое преобразование Фурье (это нужно сделать только 1 раз).
Выполняем прямое преобразование Фурье над матрицей с содержимым игрового поля.
Перемножаем каждый элемент результата на соответствующий элемент матрицы "суммирования" из пункта 1.
Выполняем обратное преобразование Фурье - и получаем матрицу с нужной нам суммой количества соседей для каждой клетки.

Весь этот процесс называется сверткой / сonvolution.

▶ Реализация на C++


//Author: Mark VandeWettering http://brainwagon.org/2012/10/11/crazy-programming-experiment-of-the-evening/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h>
#include <unistd.h>
#include <fftw3.h>
 
#define SIZE    (512)
#define SHIFT   (18)
 
fftw_complex *filter ;
fftw_complex *state ;
fftw_complex *tmp ;
fftw_complex *sum ;
 
int
main(int argc, char *argv[])
{
    fftw_plan fwd, rev, flt ;
    fftw_complex *ip, *jp ;
    int x, y, g ;
 
    srand48(getpid()) ;
 
    filter = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ;
    state = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ;
    tmp = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ;
    sum = (fftw_complex *) fftw_malloc(SIZE * SIZE * sizeof(fftw_complex)) ;
 
    flt = fftw_plan_dft_2d(SIZE, SIZE, 
                filter, filter, FFTW_FORWARD, FFTW_ESTIMATE) ;
    fwd = fftw_plan_dft_2d(SIZE, SIZE, 
                state, tmp, FFTW_FORWARD, FFTW_ESTIMATE) ;
    rev = fftw_plan_dft_2d(SIZE, SIZE, 
                tmp, sum, FFTW_BACKWARD, FFTW_ESTIMATE) ;
 
    /* initialize the state */
    for (y=0, ip=state; y<SIZE; y++) {
        for (x=0; x<SIZE; x++, ip++) {
            *ip = (fftw_complex) (lrand48() % 2) ;
        }
    }
 
    /* initialize and compute the filter */
 
    for (y=0, ip=filter; y<SIZE; y++, ip++) {
        for (x=0; x<SIZE; x++) {
            *ip = 0. ;
        }
    }
 
 
#define IDX(x, y) (((x + SIZE) % SIZE) + ((y+SIZE) % SIZE) * SIZE)
    filter[IDX(-1, -1)] = 1. ;
    filter[IDX( 0, -1)] = 1. ;
    filter[IDX( 1, -1)] = 1. ;
    filter[IDX(-1,  0)] = 1. ;
    filter[IDX( 1,  0)] = 1. ;
    filter[IDX(-1,  1)] = 1. ;
    filter[IDX( 0,  1)] = 1. ;
    filter[IDX( 1,  1)] = 1. ;
 
    fftw_execute(flt) ;
     
    for (g = 0; g < 1000; g++) {
        fprintf(stderr, "generation %03d\r", g) ;
         
        fftw_execute(fwd) ;
 
        /* convolve */
        for (y=0, ip=tmp, jp=filter; y<SIZE; y++) {
            for (x=0; x<SIZE; x++, ip++, jp++) {
                *ip *= *jp ;
            }
        }
 
        /* go back to the sums */
        fftw_execute(rev) ;
 
        for (y=0, ip=state, jp=sum; y<SIZE; y++) {
            for (x=0; x<SIZE; x++, ip++, jp++) {
                int s = (int) round(creal(*ip)) ;
                int t = ((int) round(creal(*jp))) >> SHIFT ;
                if (s) 
                    *ip = (t == 2 || t == 3) ;
                else
                    *ip = (t == 3) ;
            }
        }
 
        /* that's it!  dump the frame! */
 
        char fname[80] ;
        sprintf(fname, "frame.%04d.pgm", g) ;
        FILE *fp = fopen(fname, "wb") ;
        fprintf(fp, "P5\n%d %d\n%d\n", SIZE, SIZE, 255) ;
 
        for (y=0, ip=state; y<SIZE; y++) {
            for (x=0; x<SIZE; x++, ip++) {
                int s = ((int) creal(*ip)) ;
                fputc(255*s, fp) ;
            }
        }
 
        fclose(fp) ;
    }
    fprintf(stderr, "\n") ;
 
    return 0 ;
}

Для сборки нужна библиотека FFTW. Ключи для сборки в gcc:

gcc life.cpp -lfftw3 -lm -lstdc++

в Visual Studio нужны изменения в работе с комплексными числами.

Изображения во время выполнения алгоритма: Исходная матрица фильтра (начало координат - левый верхний угол, поле "закольцовано"):

Действительная часть фильтра после прямого БПФ:

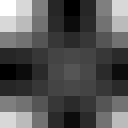
Исходное поле - 1 глайдер:

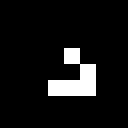
БПФ исходного поля, действительная и мнимая части:

После умножения на матрицу фильтра:

После обратного БПФ - получаем суммы:

Результат вполне ожидаемый:

"Закольцовывание" поля получается автоматически из-за БПФ.

Плюшки БПФ

Вы можете суммировать любое количество элементов с любыми коэффициентами - а время работы остается фиксированным, N²logN. Т.е. если для классической жизни - обычные алгоритмы на заполненных полях все еще достаточно быстрые, то с увеличением площади/объема суммирования - они становятся все медленнее, а скорость работы БПФ остается фиксированной.
БПФ - уже написан, отлажен и оптимизирован идеально - с использованием всех возможностей процессора : sse, sse2, avx, altivec и neon.
Вы легко можете использовать все процессоры и видеокарты взяв готовые многопроцессорные и CUDA/OpenCL реализации БПФ. Опять же, об оптимизации БПФ вам заботится не нужно. FFTW кстати поддерживает многопроцессорное выполнение (--enable-openmp во время сборки), чем больше поле - тем меньше потери на синхронизацию.
Тот же подход применим и к 3D пространству.

Сравниваем скорость работы с "наивной" реализацией

FFTW собран в режиме одинарной точности (--enable-float , дает прирост скорости примерно в 1.5 раза). Процессор - Core2Duo E8600. gcc 4.7.2 -O3


for (int i=8; i<1000; i++)
    {
        delta[i][0] = (lrand48() % 21)-10;
        delta[i][1] = (lrand48() % 21)-10;
    }

    #define NUMDELTA 18
    for(int frame=0;frame<10;frame++)
    {
        double start = ticks();
        for (y=0; y<SIZE; y++)
            for (x=0; x<SIZE; x++) 
            {
                int sum=0;
                for(int i=0;i<NUMDELTA;i++)
                    sum+=array[readpage][(SIZE+y+delta[i][0]) % SIZE][(SIZE+x+delta[i][1]) % SIZE];
                if(array[readpage][y][x])
                    array[1-readpage][y][x] = (sum>3 || sum<2)?0:1;else
                    array[1-readpage][y][x] = (sum==3)?1:0;
            }
        readpage = 1-readpage;
        printf("NaiveDelta: %10.10f\n", ticks()-start);
    }

Конфигурация теста	При каком количестве суммируемых клеток скорость FFT и наивной реализации равна
1 ядро, 512x512	29
2 ядра, 512x512	18
1 ядро, 4096x4096	88
2 ядра, 4096x4096	65

Как видим, хоть асимптотика и против FFT - но если суммировать нужно сотни и тысячи клеток - то FFT выиграет.

Update: Как оказалось, FFTW при указании флага FFTW_ESTIMATE использует далеко не оптимальные планы вычисления FFT. При указании FFTW_MEASURE - скорость сильно выросла, и ситуация выглядит уже радостнее (при суммировании менее 18 клеток - наивная реализация резко становится в 3 раза быстрее, потому тут все упирается в 18):

Конфигурация теста	При каком количестве суммируемых клеток скорость FFT и наивной реализации равна
1 ядро, 512x512	18
2 ядра, 512x512	18
1 ядро, 4096x4096	28
2 ядра, 4096x4096	19

Чтобы ни говорили - математика в программировании иногда может пригодиться в самых неожиданных местах.
И да пребудет с вами сила FFT!

18 Мая 2013